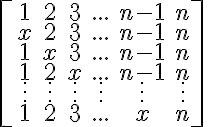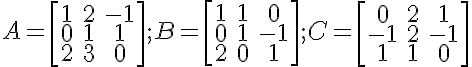LAG

Z OI wiki

	1. semestr	2. semestr	3. semestr	4. semestr	5. semestr	6. semestr
Povinné předměty	DMA ¤ LAG PR1 ¤ RPH	ALG ¤ BP1 ¤ LGR MA2 ¤ PR2	JAG ¤ PSI ¤ SPS	APO ¤ BP2 ¤ FYZ	OPT	SZZ - LS 2012
Inf. a poč. vědy			NUM ¤ OSS	DS ¤ FLP ¤ ZUI	RPZ
Počítačové syst.			EAM ¤ EM	DSP ¤ OSD	PKS ¤PSR ¤NVS
Softwarové syst.			OSS ¤ SI	ASS ¤ DS ¤ TUR	WA1
Volitelné předměty	ACM ¤ EPD ¤ ET1 ¤ FI1 ¤ HI1 ¤ HSD ¤ HT1 ¤ IA+AZK ¤ MME ¤ MMP ¤ MPS ¤ PAP ¤ PPR ¤ PRS ¤ RET ¤ SOJ ¤ UFI
Grafický minor	PGR ¤ MVR ¤ KMA ¤ MGA ¤ GRT

Info o předmětu

A0B01LAG - Lineární Algebra

Přednášející: prof. RNDr. Pavel Pták, DrSc.

Cvičící: Mgr. Michal Hroch, Mgr. Jana Šnupárková

Pravidla předmětu

Stránky předmětu na katedře matematiky

Studijní materiály

Testy v semestru

Testy a úkoly z minulých let

První test

9.11.2015

Druhý test

4.1.2016

Zkoušky

Zkoušky na Google drive

Zkouška 31. 1. 2013

Zadání

Zkouška 17. 1. 2013

1a) Najděte všechny kořeny polynomu P(x) víte-li, že má alespoň jeden celočíselný kořen.

   P(x) = x^5 - x^4 + 81x - 81

Nápověda: V průběhu řešení je možno použít Moivreovu větu.

1b) V lineárním prostoru P^3 polynomů nejvýše třetího stupně je dána množina

   M = { (x+2)^2, (x-1)^2, (x+3)^3, (x-3)^3, x, x+2 }

Ověřte, zda lineární obal M je roven prostoru P^3 a pokud ano, odeberte z množiny M takové vektory, aby výsledná množina tvořila bázi prostoru P^3.

2a) Zjistěte, pro která p ∈ R je matice A singulární. Určete hodnost matice A v závislosti na parametru p.

A =

2b) Vyřešte následující soustavu s neznámými x,y,z a parametry p,q.

   px + qy + z = p
   qx + py + z = q

3a) Zobrazení l z lineárního prostoru polynomů nejvýše třetího stupně do lineárního prostoru matic typu 2 x 2 je dáno předpisem:

   l(ax^3 + bx^2 + cx + d) = 
   Napište jeho matici vzhledem k uspořádaným bazím B a C.
   

   B = { x^3, x^3 + x^2, x^3 + x^2 + x, x^3 + x^2 + x + 1 }
   C = { , , ,  }
   S využitím této matice ukažte, že l je izomorfismus.

3b) Nechť l: L -> L' je lineární zobrazení. Dokažte: Pokud l není prosté, pak Ker(l) obsahuje nenulový vektor.

4a) Najděte normálovou rovnici roviny, která prochází danými dvěma body A a B a která je kolmá na danou rovinu p:

   A = [-1, -2, 0], B = [1, 1, 2]
   p: X=[0, 1, 1] + t(2, -1, 0) + s(0, 1, -1), t,s ∈ R

4b) Ukažte, že matice je singulární, právě tehdy když má alespoň jedno vlastní číslo rovno nule.

Zkouška 30.1.2012

1a) Zjisti koreny P(x) = x^4 + 3x^2 + 2

1b) Matice M^3,3 antisymetricka A=|aij| aij=-aji dokaz lin.podprostor a najdi bazi M

2a) Soustava rovnic s parametrem

    x +ay -z = 1
    x -2y +3z = 2
    x +y -az = 1

2b) Res soustavu

    x1 + 3x3 - x3 = 3

3a) zobr. R3->R2

   predpis: l(x1,x2,x,3)=(x1+x2-x3,2x1-x2)
   baze B = {(1,1-1),(0,2,1),(0,0,3)} B¨ = {(1,-1),(2,1)}

3b) Dokaz pokud l neni proste, pak Ker(l) neobsahuje nenulovy vektor

4a) Bod R symetricky k P podle roviny

    P [-4,5,8]
    p: 3x - 3y -4z + 25 = 0

4b) Fundamentalni system

Zkouška 24.1.2012

Zadání

Zkouška 23.1.2012

1a) Zjisti koreny P(x) = x^5 + x^4 + 81x + 81 (V prubehu je mozno pouzit Moivrovu vetu)

1b) Jsou dany LN vektory d,e,f -> d = a, e = a + b, f = a + b + c. Dokaz, ze i a, b, c jsou LN

2a) Diskutujte reseni v zavisloti na parametru a. x + y + az - 2u = -2

x + 2y + 2z +au = -3

2b) Je dana matice rozmeru n, ktera ma na vedlejsi diagonale -1, jinak je nulova. Vyjadrete determinant matice v zavislosti na n a oduvodnete.

$LaTeX: \begin{bmatrix} 0 & 0 & ... & 0 & -1 \\ 0 & 0 & ... & -1 & 0 \\ ... &... & ... & ... & ...\\ 0 & -1&... & 0& 0\\ -1 & 0 &... & 0 & 0 \end{bmatrix}$

3a) Zjisti Ker(l) a Im(l).

 l(1,0,1) = (1,1,-1,0) 
 l(0,-1,-1) = (1,0,2,1) 
 l(0,0,-1) = (3,1,3,2)

3b) Dokaz, ze 3A^2 + A + E je podobne 3B^2 + B + E, vite li, ze A a B jsou podobne.

4a) Najdete symetricky bod bodu X[3,4,2] podle primky, na ktere lezi A[2,3,-3] a B[-4,1,-7].

4b) Reste dif. rce $LaTeX: \begin{bmatrix} 1 & 1 & -1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \end{bmatrix}$ Pocatecni podminky x´(0) = (2,6,4)

Zkouška 16.1.2012

1a) Zkonstruujte realný polynom nejnižšího možného stupně, který má za kořeny čísla -2 (dvojnásobný kořen) a (1+i) (jednonásobný kořen)

1b) Čtvercová matice A, A náleží M(rozměry n,n) se nazývá magická, pokud pro A platí, že součet prvků na hlavní diagonále je roven součtu na vedlejší diagonále a tento součet je rovněž roven součtu prvků v každém řádku a každém sloupci. Označme Mag(rozměru n,n) množinu všech magických matic rozměru (n,n). Odůvodněte, proč Mag(n,n) je lineární podprostor prostoru M(n,n) a najděte dimenzi Mag(2,2)

2a) Řešte soustavu

  x1   x2    x3   x4
  1   -8    -13   9   = -9
  4   -7    -12   11  =  4
  3    1     1    2   =  13
  2   -1    -2    3   =  6    
  1    2     3   -1   =  7

2b) Jsou dány 3 vektory a,b,c (náležící) R^3 v závislosti na parametru p (p náleží R). Určete všechny p taková, aby vektory a,b,c netvořily bázi R^3.

  a = (1,p,1); b = (0,1,p); c = (p,1,0);

3a) Maticová rovnost XA = B, kde

       (2,7,3)         (1,0,2)
  A = ((3,9,4))   B = ((0,1,0))
       (1,5,3)         (0,0,1)

3b) Nechť A (náležící E^3) a p: X=B+t(a) (pro t náležící R a "a" náležící V3, "a" !=nulový vektor). Vzdálenost d(A,p) bodu od přímky se dá počítat podle formule:

           |BA x a|
  d(A,p) = -------       (BA i obě a nad sebou mají šipku, jsou to vektory)
              |a|

Dokažte tuto formuli (vlastnosti vektorového součinu jen připomeňte).

4a) Předpokládejme, že lineární zobrazení l: R^4 -> R^3 má vůči standarním bázím matici zobrazení A.

       (1,-1,0,2)
  A = ((2, 1,1,1))
       (4,-1,1,5)

Určete bázi Ker(l) a Im(l).

4b) Dokažte následující tvrzení: Pokud jsou matice A,B podobné, pak jsou podobné i matice (A^2 + A + E) a (B^2 + B + E).

Zkouška 8.2.2011

1a Najít kořeny polynomu hornerovým schematem. Polynom se mi nějak nevešel na fotku, takže nevím, jak vypadal. Kořeny byla celá čísla.

1b Nechť L je lineární prostor, a vektory a, b, c jsou lineárně nezávislé vektory z L. Utvořme vektory

  d = a - 3b + 2c, 
  e = 2a + b - 4c, 
  f = -2a +3b - c

určete, zda jsou vektory d, e, f lineárně závislé nebo nezávislé. Své kroky vysvětlete, strohý výpočet nestačí. Pokud používáte nějakou matematickou větu, zformulujte ji a ověřte její předpoklady.

2a řešte maticovou rovnost XA + X = O kde O je nulová matice (všude nuly) a

A = $LaTeX: \begin{bmatrix} 2 & 2 & 1 \\ 2 & 0 & 3 \\ 0 & 1 & 1 \end{bmatrix}$

Výpočítejte pomocí vhodné inverzní matice. Tu hledejte determinantovou metodou.

2b řešte soustavu bohužel nekvalitní fotka, nemůžu to přečíst. Byla to homogenní soustava 4 rovnic, 5 neznámých, hodnost myslím 3.

Tvoří množina všech řešení lin. podprostor R5? Pozor: otázka byla položena přesně takto, ale odpověď bylo potřeba i zdůvodnit.

3a Lineární zobrazení l: R2 -> R3. Vůči bázím B1:{(2, 1), (3, 2)} a B2: {(4, 2, -1), (3, 1, 3), (2, 1, 0)}

A = $LaTeX: \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ 1 & 0 \end{bmatrix}$

Spočítat l(3, 1)

3b Definujte inverzní matici. Dokažte, že je určená jednoznačně.

4a Jsou dány body A, B, C: A = [3, 1, -2] B = [4, 2, 0] C = [-1, 3, -3]

dokažte, že tvoří trojúhelník a spočítejte jeho obsah. Nápověda: Veďte přímku AB a najděte vzdálenost přímky od C.

4b řešte soustavu diferenciálníc rovnic.:

A = $LaTeX: \begin{bmatrix} 5 & -2 & 2 \\ -1 & 4 & -1 \\ -4 & 4 & -1 \end{bmatrix}$

(není tam řetízek)

Zkouška 1.2.2011

1a P(x) = 5x^5 – 4x^4 + 80x + 16 Overit zda 1/5 je koren a pak najit všechny koreny.

1b Dokazat P(a) (nad tim celym je pruh) = P(a) (jen nad tim a je pruh)

2a najit reseni

  2  6  6  9 | 7
-14 -2  6 -3 | -13
 -7  4  9  6 | -2 
  3  4  3  6 | 6 
 -9 -2  3 -3 |-9

2b Spocitat determinant

Aii = i Aij = 2

  |1 2 2 . . . 2 2| 
  |2 2 2 . . . 2 2| 
  |2 2 3 . . . 2 2| 
  |.   ..        .| 
  |.      ..     .| 
  |2 2 . . . n-1 2| 
  |2 2 . . . 2   n|

Je to matice n,n

3a

 l(1,0,0) = (2,3) 
 l(0,1,0) = (1,-2) 
 l(0,0,1) = (-1,1)

overit zda je „na“ najit všechny vzory vektoru v=(3,1)

3b Matice typu (2,2) Plati l(X) det(X)

Dokazat, zda je zobrazeni linearni

4a Bodem A vest primku protínajíci a,b

 A = [2,0,2] 
 a: X = [3,-1,0] + s(1,-,1,0) 
 b: Y = [3,3,-1] + t(1,1,-1)

4b

  x1’ = -3x1 – x2 
  x2’ =   x1 – x2

najit fundamentalni system

Zkouška 11.1.2011

1A Napsat koreny polynoma: (vysledky: 2, -3, 1+i, 1-i)

        x^4 - x^3 -6x^2 + 14x -12

1B P5 je linearni prostor polynoma stupne <= 5. Necht' je P mnozina vsechnych polynoma z P5 ktery jsou delitelni s (x^2+1). Dokazte, ze je P linearni podprostor prostora P5.

2A Soustava s 5 nezamych a 4 rovnice (mela hodnotu 2)

2B Podobne jako vzor 3 / 2A, jenom tam bylo α misto -α pro B

3A Mame primky:

          p: X = [2, -5, 1] + t(3,-2,-1)
          q: Y = [5, 5, 11] + u(2, 3, 5)

Dokazat ze jsou mimobezky a najit jeho pricku pres bodu M = [-4, -5, 3]

3B Pres souradnicich dokazte ze u x v je kolme na u, kde jsou u a v vektory z V^3

4A Linearne zobrazeni je dano predpisem:

          l(0, 1, 1) = 3
          l(0, 1, -1) = 1
          l(2, 0, 1) = -1

Spocitat l(3, 4, 5). Najit bazy Ker(l) a Im(l).

4B Diferencialni rovnice:

           x1' = x1 + 2x2
           x2' = 2x1 + x2
          
           x1(0) = -1; x2(0)=2

Zkouška 5.2.2010

To samé, co 3.2. :)

Zkouška 3.2.2010

1A Pomocou hornera zistite hodnotu polynomu v bode 3.

1B Dokážte, že v polynome

        P(x) = a^6x^6  +  a^5x^5  +  ..  +  ax  +  a0

r deli a0, ak viete, ze r je koreň polynomu.

2A Normálna sústava rovníc o 5tich neznámich (3 riadky matice boli lin. závislé).

2B Na zákl. vlastností determinantu uvažujte hodnosť matice v závislosti na parametre p z R.

3A Maticová rovnosť AX=B.

3B Príklad podobný vzoru 2 / 3a) (http://math.feld.cvut.cz/hroch/vyuka/materialy/vzor.pdf)

4A Ako vzor 1/4a), neurčovalo sa či je zobraz. defin. korektne; ale spočítajte l(3,4,5) + nájsť bázu Ker(l) a Im(l).

4B Diferencialna rovnica, zadanie zo vzoru 2/pr.4b), pociatoč. podm. iné.

Zkouška 27.1.2010

1A Zostaviť polynom, ak viete že má korene 3 a 1+j

1B Nájsť bázu lineárneho priestoru matíc, ktoré mali tú vlastnosť, že súčet všetkých členov v ich riadku aj stĺpci aj na diagonálach bol rovnaký.

2A Normálna sústava rovníc o 5tich neznámich (3 riadky matice boli lin. závislé).

2B Boli zadané 4 vektory z R3 a každý mal jeden parameter - trebalo zistiť pre akú hodnotu parametra budú tie vektory LN.

3A Maticová rovnosť AX=B.

3B Dokázať vzorec na výpočet vzdielanosti bodu od priamky (Pták 4.5.3).

4A Nájsť kernel a image zobrazenia, ktoré bolo zadané normálnym predpisom.

4B Dokázať nejakú blbosť čo sa týkala podobnosti matíc :-).

Zkouška 25.1.2010

1A Užitím Hornera ukažte, že -2 je kořenem polynomu p(x)=x⁶+x⁵-11x⁴-13x³+26x²+20x-24 s násobností 3. Najděte všechny kořeny.

1B Ukažte,že neexistuje polynom, který by se rovnal funkci e^x na celém R. Může se e^x rovnat polynomu na něakém intervalu? (lze použít i výsledků diferencionálního počtu)

2A Řešení 3 rovin v závisloti na dvou parametrech.

2B Determinant matice, kde neznámá x byla pod diagonální maticí.

3A Zjistit pro jaká a existuje inverzní matice a tuto inverzní matici spočítat:

$LaTeX: \begin{bmatrix} 0 & 1 & a \\ 1 & 0 & a \\ 0 & 0 & -1 \end{bmatrix}$

3B Dvě přímky, zjistit, zda jsou mimoběžky; určit, jak se musí změnit jeden z bodů, aby byly rovnoběžné.

4A Lineární transformace zadaná dvěma vektory a Ker(l). Zjistit obraz určeného vektoru a určit její matici (NUTNO DOPLNIT).

4B Řešit diferenciální rovnici x'= Ax, kde

$LaTeX: A=\begin{bmatrix}2&-1\\1&0\end{bmatrix}$

Zkouška 22.1.2010

1A Užitím Hornera ukažte, že komplexní číslo j (komplexní jednotka) je kořenem polynomu p(x)=x⁴+3x²+2. Najděte všechny kořeny.

1B Je dán prostor antisymetrických matic 3x3 kde Aij=-Aij pro všechna i ≠ j. Jedná se o lineární podprostor prostoru všech matic 3x3? Najděte bázi.

2A Maticová rovnice: XA-B=XC

2B Spočtěte determinant matice A (5x5 a má vyjít -997 myslim).

$LaTeX: A = \begin{bmatrix}-2 & 1 &-3& -1 & 5\\1&-5&1&0&5\\1&3&-3&-1&4\\2&0&1&3&0\\-4&0&2&-1&0\end{bmatrix}$

3A Lineární zobrazení z R³ do R³:
l(4,0,-1) = (1,-1,1)
l(3,-1,1) = (0,1,2)
l(1,2,3) = (1,1,5)
Najděte Ker(l). Patří (1,1,3) do Img(l) ? (nepatří btw...)

3B Zobrazení l:z L do L s čarou je prosté. a {b1,b2,...,bn} je báze L. Dokažte, že {l(b1),l(b2),...,l(bn)} je báze Img(l).

4A Jsou dány přímky :
p: [-5,5,1]+t(3,2,-2)
q: [9,0,2]+u(6,-2,-1)
Ukažte, že se jedná o různoběžky a určete jejich vzdálenost.

4B Je dána matice zobrazení (3x3):

$LaTeX: A = \begin{bmatrix}1&-1&1\\1&1&-1\\0&-1&2\end{bmatrix}$

Najděte fundamentální systém. (je tam řetízek).

Zkouška 15.1.2010

1A Užitím Hornera ukažte, že komplexní číslo j (komplexní jednotka) je kořenem polynomu (konkrétní polynom 6. stupně). Jsou další kořeny reálné?

1B a,b,c vektory z lin. prostoru L
d=a
e=a+b
f=a+b+c
dokažte, že <a,b,c>=<d,e,f>, (d,e,f jsou taky vektory), lze použít tvrzení o stabilitě lineárního obalu

2A klasická soustava 3 rovnice, 3 neznámé, pravá strana
pomocí A^-1 najděte řešení a potvrďte ho Cramerem

2B soustava v R⁵ o jedné rovnici (s pravou stranou).
Vyřešte soustavu. Je množina všech řešení lineární podprostor v R⁵? Zdůvodněte.

3A Je dáno zrcadlo (rovina) a 2 body M,N na téže straně zrcadla. Předpokládejme, že paprsek prochází bodem M. Ve kterém bodě se musí odrazit, aby procházel i bodem N?

3B V souřadnicích dokažte, že $LaTeX: u \times v$ je kolmý na u. (u,v jsou vektory z V₃, $LaTeX: \times$ je vektorový součin)

4A Dána matice lin. zobrazení (R³->R²) typu 2,3, báze B (3 vektory z R³) a báze B' (2 vektory z R²). Určete Ker(l).

4B Dokažte, že relace podobnosti matice je tranzitivní.

Zkouška 13.1.2010

1A Napiš a dokaž Moivrovu větu

1B pomocí Moivrovi věty vypočti x na 4 + 16 = 0

2A soustava rovnic, měla defect 3, napsat řešení

2B jsou dvě matice s parametry, diskutujte hodnost C = B + A² + A³ + ... + A⁷ v závislosti na parametru

3A Maticová rovnice ve tvaru XA = C zadané A i C vypočíst

3B víme, že číslo, číslo, číslo je dělitelné 19, aniž byste počítali determinat ukažte, že je dělitelný 19 - stejný příklad jako v těch návodných, jen ta matice byla transponovaná

4A bod, rovina, najít symetrický bod vzhledem k té rovině

4B soustava diferenciálních rovnic, ale jen dvě o dvouch. Bylo tam třeba vytvořit řetěz vlastních vektorů

Zkouška 11.1.2010

1A P(x)=x⁴ - x³ - 6x² + 14x - 12 Viete ze tento polynom ma presne 2 cele korene, najdite vsechy korene

1B necht P5 je prostor polynomu so stupnom 5 alebo menej. nech P je podmnozina P₅. a vsechny polynomy z P jsou delitelne polynomem (x2-1). Je P podprostor prostoru P₅? zduvodnete.

2A rieste rovnicu AX + A + X= 0 kde 0 je nulova matica

2B sustava 3 linearnych rovnic (3 nezname) s parametrom a a b (klasika to iste troch rovin, ale bez geometrickecho chapania)

3A su dane 2 priamky a bod A , najdite priamku ktora pretina obe zadane priamky cez bod A

3B dokazte ze plati : $LaTeX: a \times (b \times c)=(a c)b - (a b)c$

4A dane je linearne zobrazeni z R³ do R⁴. Najdite Ker(l)

     l(1,0, 1) = (1,1,-1,0)
     l(0,1,-1) = (1,0, 2,1)
     l(0,0, 1) = (3,1, 3,2)

4B rieste diferencialnu rovnicu x´=Ax, kde

$LaTeX: A = \begin{bmatrix}-1&1&1\\1&-1&1\\1&1&-1\end{bmatrix}$

LAG